SageMath 版本信息

> sage
┌────────────────────────────────────────────────────────────────────┐
│ SageMath version 10.1.beta3, Release Date: 2023-06-11              │
│ Using Python 3.11.1. Type "help()" for help.                       │
└────────────────────────────────────────────────────────────────────┘
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ Warning: this is a prerelease version, and it may be unstable.     ┃
┗━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┛
sage:

• 此前对 $x$ 开 $n$ 次方, 常用 pow(x, 1/n), 但对于结果不是整数时就得用 gmpy2.iroot(x, n), 而我又不喜欢使用第三方库, 现在对此问题有了以下解决方案

Sage

n = 3  # 例如，开三次方
x = 27. # 表示待开方的数, .表示浮点数
# result = power_mod(x, 1/n, x)  # 对整数x开n次方，不保留小数
result = real_nth_root(x, n)
print(result)
# sage 保留整数部分
int(result)

素数支持

素数序列

Sage

Primes()

Output

Set of all prime numbers: 2, 3, 5, 7, ...

素性检测

Sage

5.is_prime()
is_prime(5) # 与上一行等价
# 或者使用下面两行
P = Primes()
5 in P

Output

True

下一位素数, 仅支持传递整数参数

Shell

sage: P.next(5)
7
sage: P.next(6)
7

返回第 n 个质数

Shell

sage: P = Primes()
sage: P.unrank(0)
2
sage: P.unrank(3)
7

分解合数

Sage

factor(5 ** 2 * 3)

Output

3 * 5^2

椭圆曲线支持

Sage

a = -3
b = 3
ecc = EllipticCurve([a, b])
show(ecc)
ecc.plot()

Output

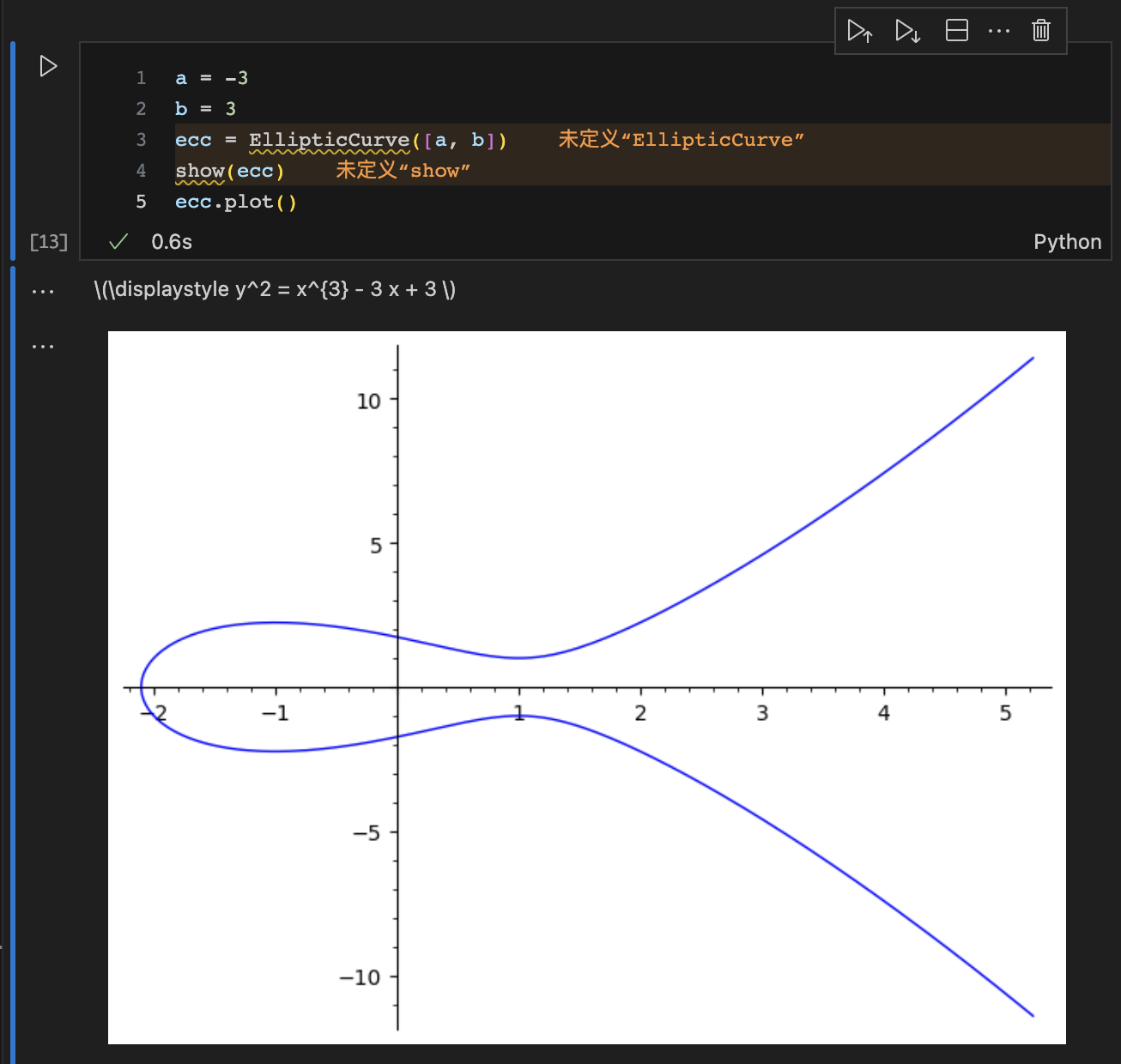
有限域上的椭圆曲线

Sage

# y**2 = x**3 + a*x + b
a = -3 
b = 3
p = 17
E = EllipticCurve(GF(p), [a, b])
print(E)

Output

Elliptic Curve defined by y^2 = x^3 + 14*x + 3 over Finite Field of size 17

运算(待续)

点的相加

Shell

点的相乘

Shell

椭圆曲线的阶

Shell

sage: a = -3
....: b = 3
....: p = 17
....: ecc = EllipticCurve(GF(p), [a, b])
....: ecc.order()
23

解方程

LaTeX 支持

Sage

latex(E)

Output

y^2 = x^{3} + 14 x + 3

在输出两端加上 $ $ , 放入可以解析 markdown 的程序, 即可呈现 latex 公式, 例如: $y^2 = x^{3} + 14 x + 3$