LOV3

1.2 XOR

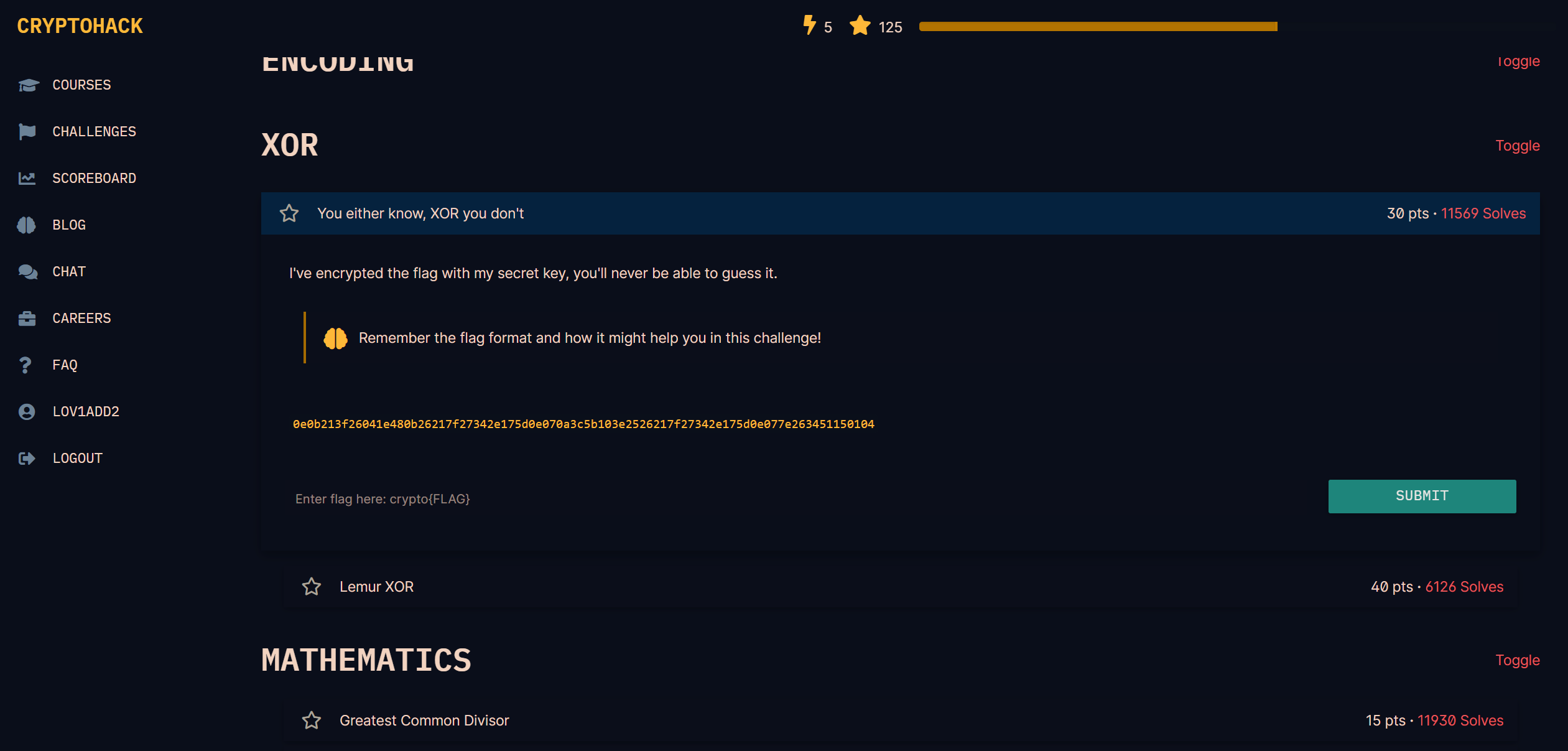
挑战 1.2.4 XOR -> You either know, XOR you don't

发现之前做了点了 隐藏一下已经解决的

from pwn import xor
from Crypto.Util.number import long_to_bytes as l2b

c = "0e0b213f26041e480b26217f27342e175d0e070a3c5b103e2526217f27342e175d0e077e263451150104"
c = l2b(int(c, 16)) # hex to int to bytes
# 已知flag 前几位为crypto{ 于是与这几位结果对应密文xor即可得出key
flag_begin_format = b"crypto{"
flag_end_format = b"}"
key = xor(c[:7], flag_begin_format) + xor(c[-1:], flag_end_format)
print(xor(c, key))

拿到flag solve~

---

挑战 1.2.5 XOR -> Lemur XOR

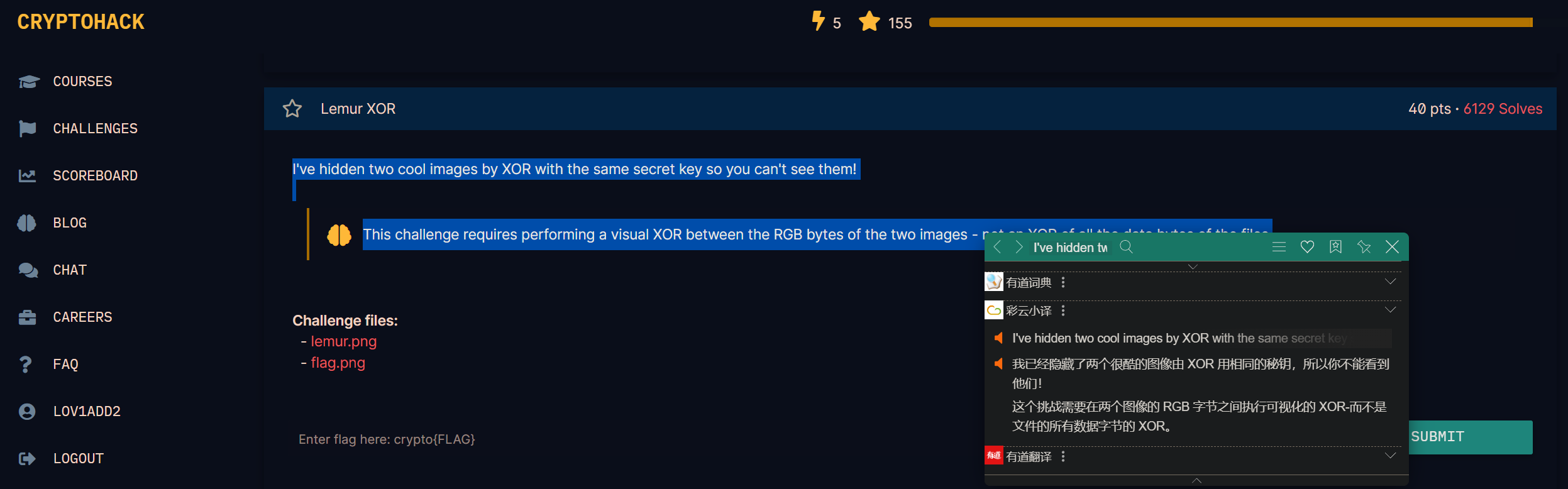
翻译了下描述 盲猜图片异或

描述表明在RGB bytes(而不是全部)下用了同样的密钥 XOR 出了给出的两张图片

首先来回顾一下 XOR 性质

1. 交换律

$A \bigoplus B = B \bigoplus A$

2. 结合律

$A \bigoplus (B \bigoplus C) = (A \bigoplus B) \bigoplus C$

3. 恒等率

$A \bigoplus 0 = A$

4. 归零率

$A \bigoplus A = 0$

5. 自反

$A \bigoplus B \bigoplus B = A \bigoplus 0 = A$

---

基于这些性质 我们可以对题目做出如下处理

imageF 和 imageL 简写为 $F$ 和 $L$, $A$ 和 $B$ 为两图片分别 XOR $K$ 的结果

$F \bigoplus K = A$

$L \bigoplus K = B$

对两式左右两边同时 XOR

$F \bigoplus K \bigoplus L \bigoplus K = A \bigoplus B$

由于 XOR 满足交换律

$F \bigoplus L \bigoplus K \bigoplus K = A \bigoplus B$

由于 XOR 满足结合律

$F \bigoplus L \bigoplus (K \bigoplus K) = A \bigoplus B$

简化

$F \bigoplus L = A \bigoplus B$

于是推出两图 XOR 的结果 $= A \bigoplus B$ 也就是上式

exp

from pwn import xor
from PIL import Image
import numpy

pathF = "Python\\CTF\\CryptoHack\\1.2.5XOR\\flag_7ae18c704272532658c10b5faad06d74.png"
pathL = "Python\\CTF\\CryptoHack\\1.2.5XOR\\lemur_ed66878c338e662d3473f0d98eedbd0d.png"

with open(pathF, "rb") as f:
    flag = f.read()
with open(pathL, "rb") as f:
    lemur = f.read()

l = Image.open(pathL)
f = Image.open(pathF)

nl = numpy.array(l) # 3D array
nf = numpy.array(f) # 3D array
# print(nl.shape) # (height, width, 3)
Image.fromarray(nl ^ nf).show()
# 密文攻击 对每个像素的RGB值 进行异或运算得出两图xor后的图像
# flagR = flag[0::3]
# flagG = flag[1::3]
# flagB = flag[2::3]
# lemurR = lemur[0::3]
# lemurG = lemur[1::3]
# lemurB = lemur[2::3]
# print(xor(flagR, lemurR))

注释掉的是我不想用库 想直接做 但发现行不通..

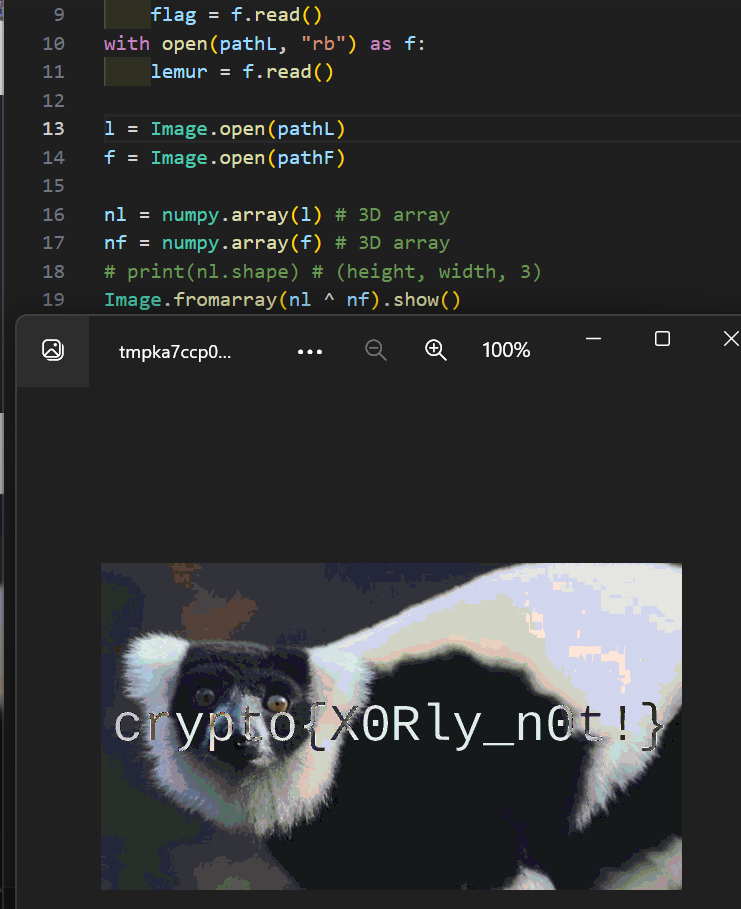
拿到flag solve~

---

1.3 MATHEMATICS

挑战 1.3.1 -> Greatest Common Divisor

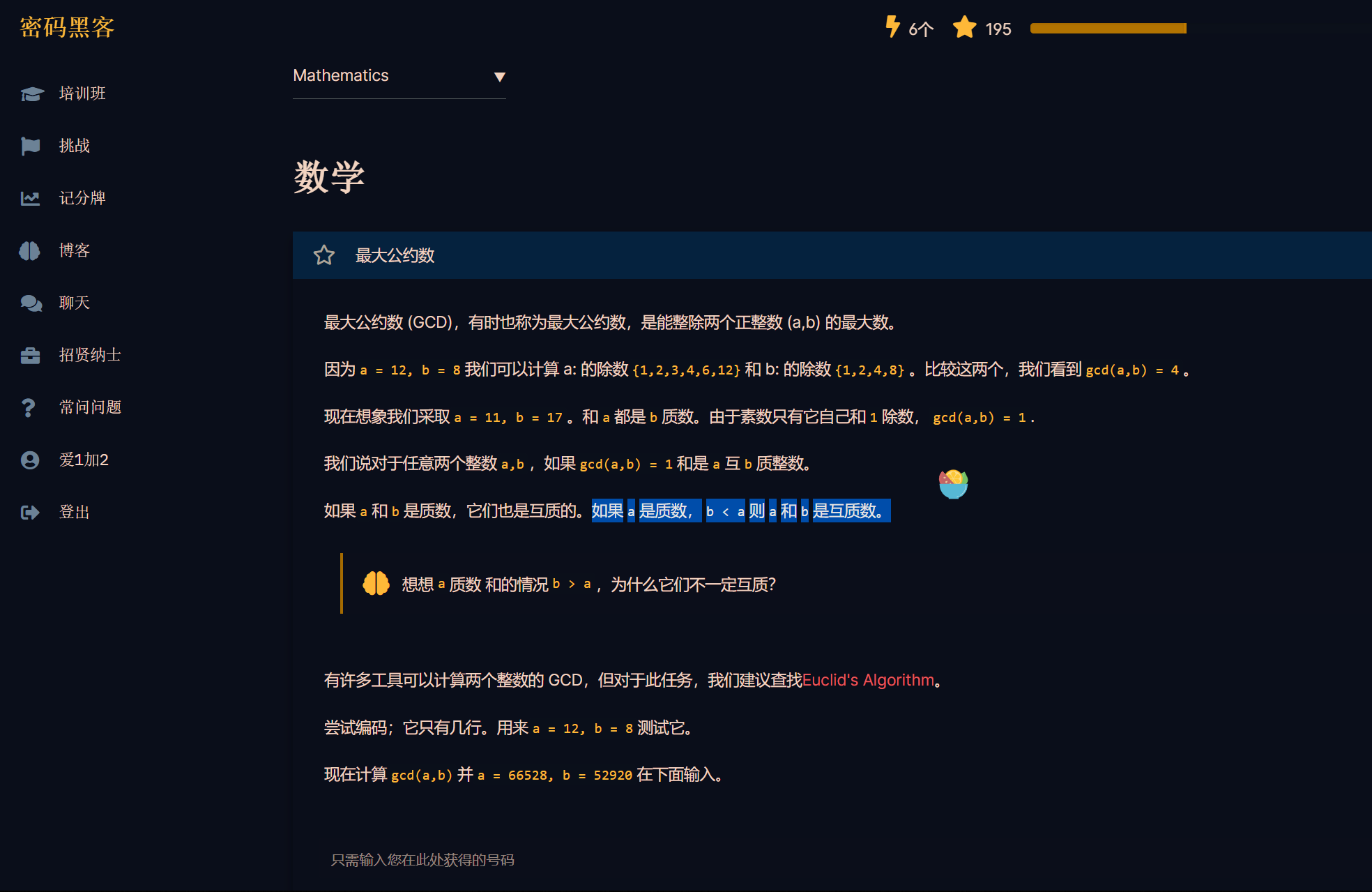
看了题目描述后就是让算出两数的 gcd(最大公约数)后输出 同时题目给出了一个思考问题

如果 a 和 b 都是质数，它们也是互质的。如果 a 是质数且 b < a，则 a 和 b 是互质的。
考虑 a 是质数且 b > a 的情况，为什么它们不一定互质？
有很多工具可以计算两个整数的最大公因数，但是在这个任务中，我们建议查找 欧几里得算法 进行计算。

维基百科上的这张图很直观

这题如果直接用 __gcd() 那就太水了，我们来手写一下两种算 gcd 的函数

import gmpy2
from Crypto.Util.number import getPrime

a = getPrime(10)
b = getPrime(10)
# 如果 a 和 b 都是质数(且a != b)，它们也是互质的。
"""
while 1:
    if gmpy2.gcd(a,b) == 1:
        # print("a 和 b 是互质的，重新生成")
        a = getPrime(10)
        b = getPrime(10)
        pass
    else:
        print("a ->", a)
        print("b ->", b)
        break
"""
print("如果 a 和 b 都是质数，它们也是互质的 ->", gmpy2.gcd(a,b)) # 1
# 如果 a 是质数且 b < a，则 a 和 b 是互质的。
flag = 0
for _ in range(a):
    if gmpy2.gcd(a, _) == 1:
        flag += 1
if flag == a-1:
    print("如果 a 是质数且 b < a，则 a 和 b 是互质的")
    # 考虑 a 是质数且 b > a 的情况，为什么它们不一定互质？
    print("这是因为质数的最大公因数只能是 1，而小于 a 的正整数中除了 1 以外，没有和 a 同时为质数的数，因此它只能与小于 a 的正整数互质。")
else:
    print("error")
# 有很多工具可以计算两个整数的最大公因数，但是在这个任务中，我们建议查找欧几里得算法进行计算。
def GreatestCommonDivisor(n1, n2):
    if n1 < n2:
        n1, n2 = n2, n1
    while n2 != 0:
        remainder = n1 % n2
        n1 = n2
        n2 = remainder
    return n1

def GreatestCommonDivisorV2(n1, n2):
    if n1 == 0:
        return n2
    while n2 != 0:
        if n1 > n2:
            n1 -= n2
        else:
            n2 -= n1
    return n1

def GreatestCommonDivisorV3(n1, n2):
    if n2 == 0:
        return n1
    else:
        return GreatestCommonDivisorV3(n2, n1 % n2)

print(GreatestCommonDivisor(52920 ,66528))
print(GreatestCommonDivisorV2(52920 ,66528))
print(GreatestCommonDivisorV3(52920 ,66528))

solve

---

挑战 1.3.2 -> Extended GCD

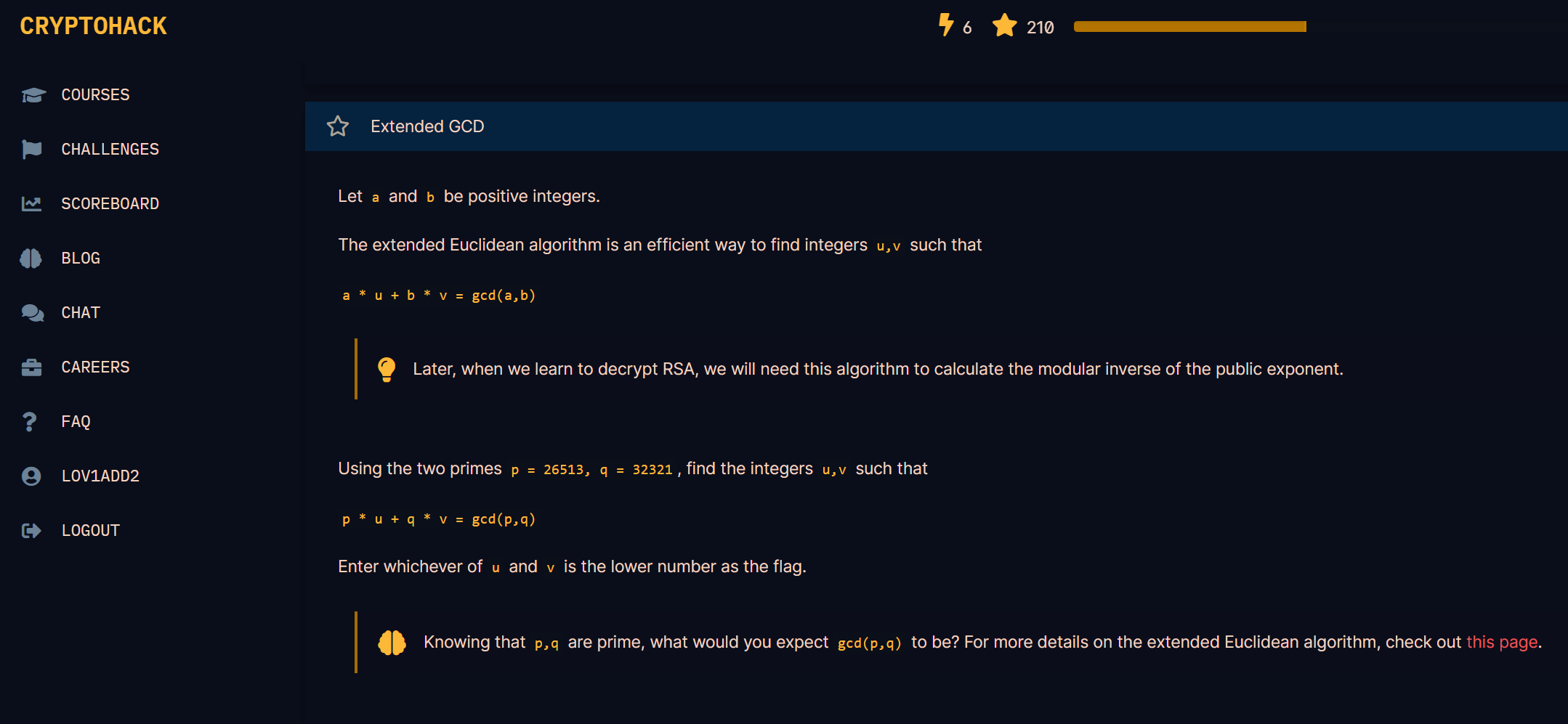
一眼拓展欧几里得(废话)

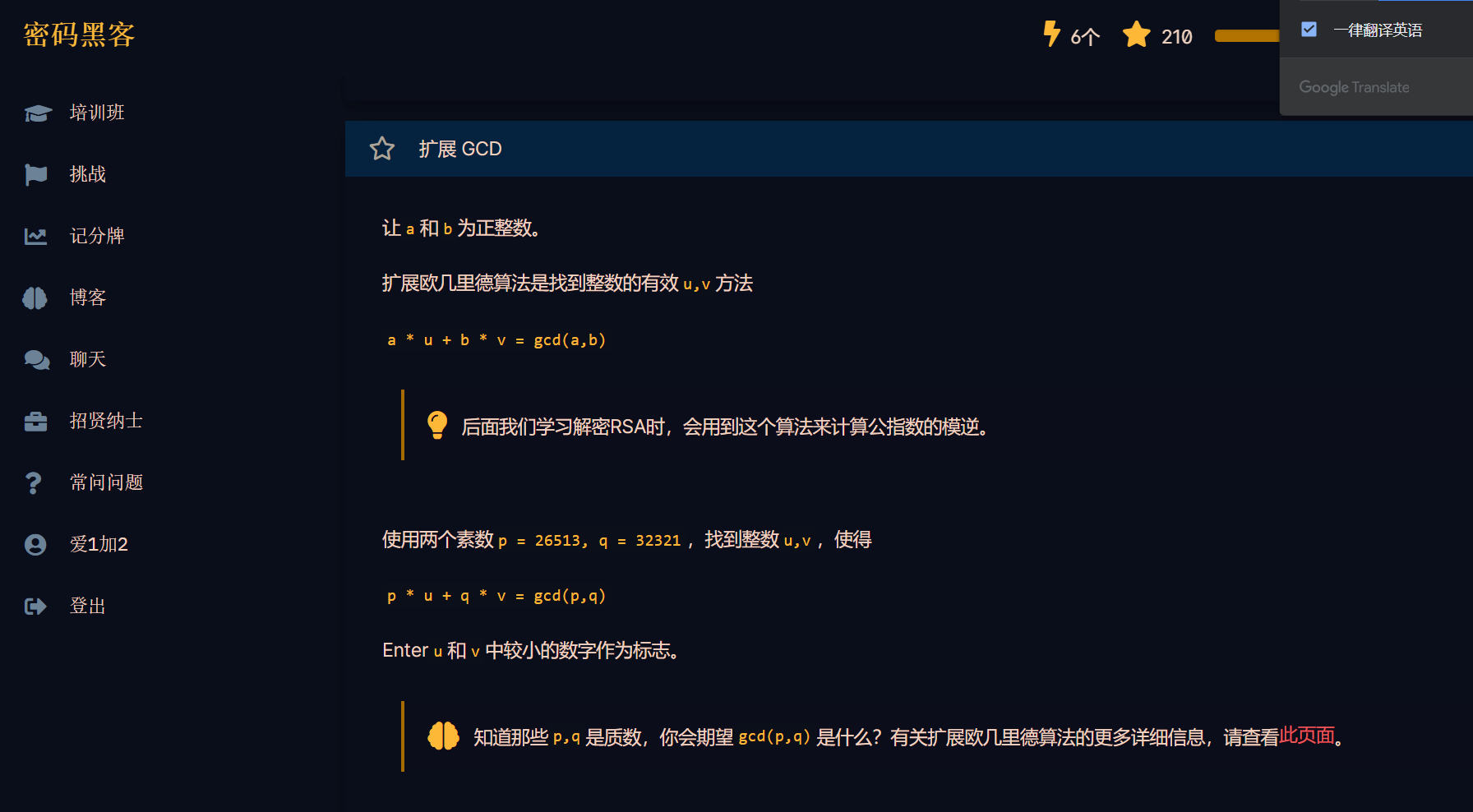
好吧还是中文顺眼点(其实就是看不懂英格利希)

不得不说这讲的很清晰啊，完全可以跟着网站的教程做了再去看数论书，或许会更快些

EXgcd 最关键的就是这个式子

$a \times u + b \times v = gcd(a,b)$

拓展欧几里得 所做的就是在有 $a$ 和 $b$ 时能求出其两者的系数 也就是上式的 $u$ 和 $v$

p = 26513
q = 32321

def extended_gcd(a, b):
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = extended_gcd(b % a, a)
        return (g, x - (b // a) * y, y)
    
u, v = extended_gcd(p, q)[1:]
print(u, v) # 10245 -8404

题目需要提交 $u$ 和 $v$ 中较小的那个数

于是我们输入 -8404 solve~

话说有人push真好啊，不是老大监督可能今天就摸了..

---

挑战 1.3.3 -> Modular Arithmetic 1

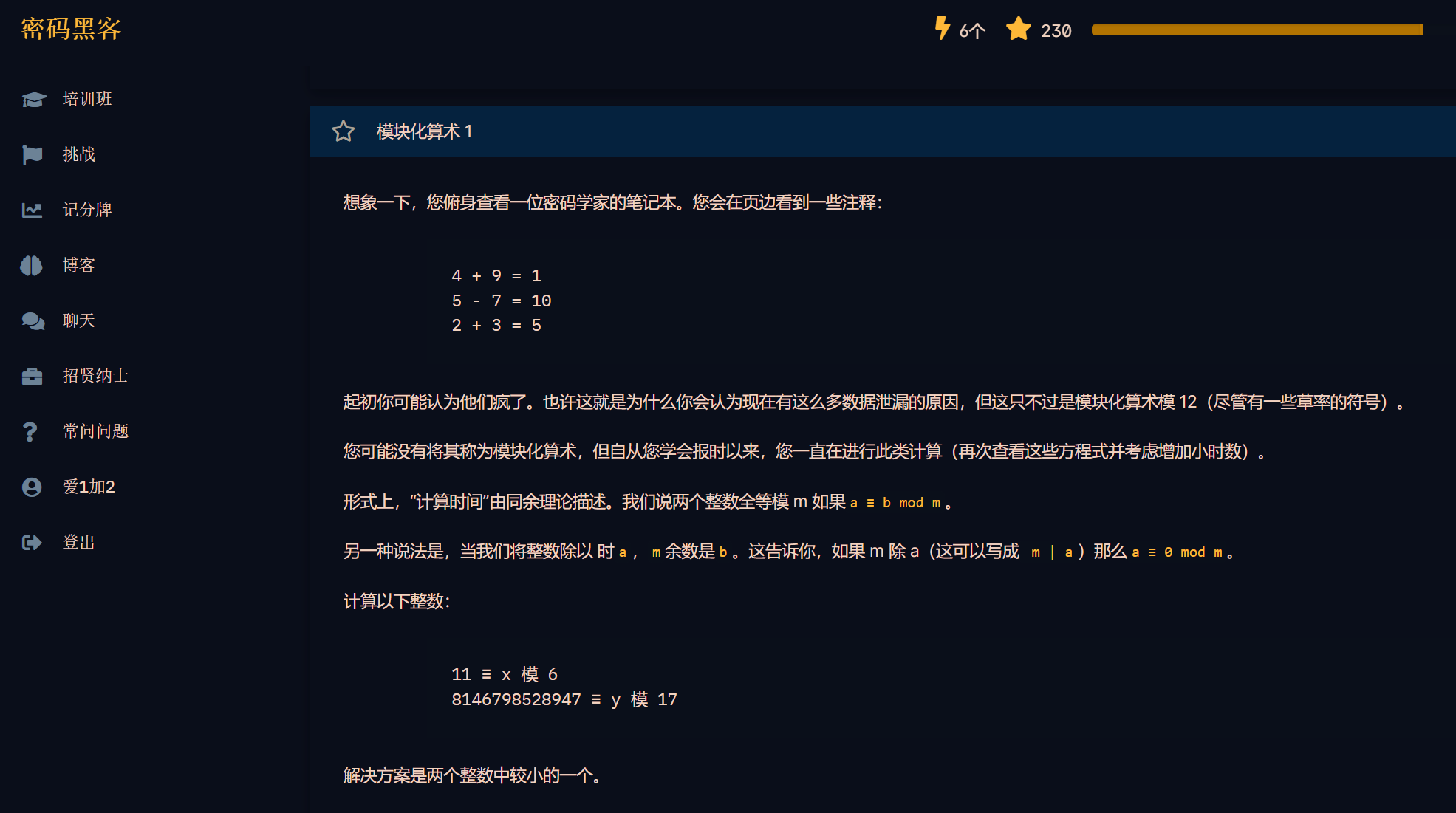
模算数入门

# 11 ≡ x mod 6
print(11 % 6) # 5
# 8146798528947 ≡ y mod 17
print(8146798528947 % 17) # 4

题目让回答两个整数中较小的那个 输入 4 solve~

---

挑战 1.3.4 -> Modular Arithmetic 2

模算数2

# p = # is prime
# 整数模p定义一个字段：Fp
# 如果模不是素数，则整数模 n 的集合定义一个环。
# 有限域 Fp 是整数{0,1，... ，p-1}的集合，在加法和乘法下，集合中的每个元素 a 都有一个逆元素 b，这样 a + b = 0和 a * b = 1。
# 请注意，用于加法和乘法的标识元素是不同的！这是因为当使用操作符时，标识应该什么都不做: a + 0 = a 和 a * 1 = a。
# 假设我们选择 p = 17，计算3^(17) mod 17，现在同样使用5^(17) mod 17。
print(pow(3, 17, 17)) # 3
print(pow(5, 17, 17)) # 5
# 试着计算 7^(17) mod 17
print(pow(7, 17, 17)) # 7
# 这个有趣的事实被称为费马小定理。当我们研究 RSA 密码学时，我们将需要这个(及其概括)。
# 现在取质数 p = 65537，计算 273246787654 ^ (65536) mod 65537
# tips:你需要计算器吗
print(pow(273246787654, 65536, 65537)) # 1 

于是我们输入 1 solve~

---

挑战 1.3.5 -> Modular Inverting

# tags:乘法逆元, 模逆
# 正如我们所看到的，我们可以在一个有限域Fp内工作，对元素进行加法和乘法，并且总是获得该域的另一个元素。
# 对于场中的所有元素g，存在一个唯一的整数d，使得g * d ≡ 1 mod p。
# 这是g的乘法逆
# 如：7 * 8 = 56 ≡ 1 mod 11
# 什么是倒数元素： 3 * d ≡ 1 mod 13?
# 想想我们刚才的那个小定理。它是如何帮助你找到一个元素的逆的？
def extended_gcd(a, b):
    """
    使用扩展欧几里得算法计算gcd(a, b), 同时记录过程中系数x, y,满足ax+by=gcd(a,b)
    """
    if b == 0:
        return a, 1, 0
    gcd, x1, y1 = extended_gcd(b, a % b)
    x = y1
    y = x1-(a//b)*y1
    return gcd, x, y


def mod_inv(a, m):
    """
    计算模m下a的逆,即a关于m的乘法逆元
    """
    # 使用扩展欧几里得算法计算gcd(a, m), 同时记录过程中系数x, y
    gcd, x, y = extended_gcd(a, m)

    # 如果a和m不互质,不存在逆元
    if gcd != 1:
        raise ValueError(f"{a} 和 {m} 不互质,不存在逆元")

    # 由于x可能为负数,因此需要加上m并取模
    return (x % m+m) % m


print(mod_inv(3, 13)) #9

于是我们输入 9 solve~

---

1.4 DATA FORMATS

挑战 1.4.1 -> Privacy-Enhanced Mail?

from Crypto.PublicKey import RSA

path = b"D:\\Document\\Code\\Python\\CTF\\CryptoHack\\1.4DATA-FORMATS\\privacy_enhanced_mail_1f696c053d76a78c2c531bb013a92d4a.pem"
# 从这个 PEM 格式的 RSA 密钥中提取私有密钥 d 作为十进制整数。
with open(path, "rb") as f:
    key = RSA.importKey(f.read())
    print(key.d)

solve~

---

挑战 1.4.2 -> CERTainly not

# 正如在之前的挑战中提到的，PEM 只是 DER 编码的 ASN.1 之上的一个很好的包装器。在某些情况下，您可能会直接遇到 DER 文件；例如，许多 Windows 实用程序默认情况下更喜欢使用 DER 文件。但是，其他工具需要 PEM 格式并且难以导入 DER 文件，因此最好知道如何将一种格式转换为另一种格式。
# SSL 证书是现代网络的重要组成部分，它将加密密钥绑定到有关组织的详细信息。我们将在 TLS 类别中详细介绍这些和 PKI。此处显示的是 DER 编码的 x509 RSA 证书。找出证书的模数，以小数形式给出答案。
from Crypto.PublicKey import RSA
path = b"D:\\Document\\Code\\Python\\CTF\\CryptoHack\\1.4DATA-FORMATS\\2048b-rsa-example-cert_3220bd92e30015fe4fbeb84a755e7ca5.der"
with open(path, "rb") as f:
    key = RSA.importKey(f.read())
    print(key.n)

solve~

---

挑战 1.4.3 -> SSH Keys

题目英文含义为从 .pub 文件中读取模数 n

from Crypto.PublicKey import RSA
path = r"D:\Document\Code\Python\CTF\CryptoHack\1.4DATA-FORMATS\bruce_rsa_6e7ecd53b443a97013397b1a1ea30e14.pub"
with open(path, "rb") as f:
    key = RSA.importKey(f.read())
    print(key.n)

solve~

---

挑战 1.4.4 -> Transparency

密钥文件可以解析出 $n$ 与 $e$，但 $n$ 是一个巨大的数

搜索wp后发现别人使用 Maltag 分析域名 我搜了下发现不会用，于是想着既然是域名，那用 Fofa 应该也差不多，结果：

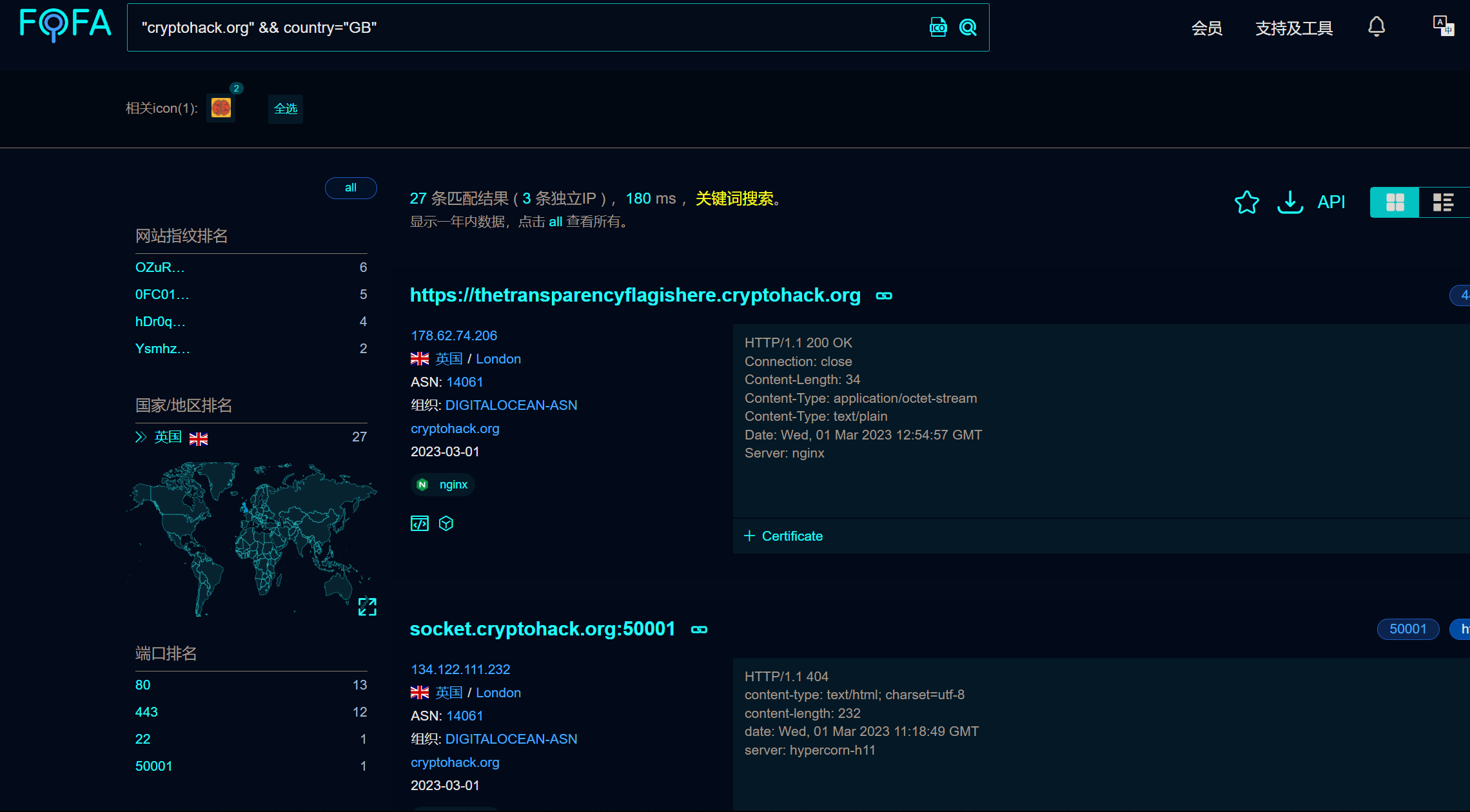
语法

"cryptohack.org" && country="GB"

即可 国籍是因为看到查到的来自于 *.cryptohack.org 的域名均为英国 于是加上国籍属性后，检索结果的第二页即可看到

solve~

---

2 MATHEMATICS

2.0 MODULAR MATH

挑战 2.0.1 Quadratic Residues

二次剩余 的引入

我们已经研究过同余关系中的乘法和除法，但是把平方根模取为一个整数意味着什么呢？

对于下面的讨论，让我们研究模 $p = 29$。我们可以取整数 $a = 11$并计算 $a^2 = 5 \pmod {29}$。

当 $a = 11$，$a^2 = 5$ 时，我们说 5 的算术平方根是11。

这感觉不错，但现在让我们想想18的平方根。从上面的例子中，我们知道我们需要找到一个整数 a，使得 a2 = 18

您的第一个想法可能是从 $a = 1$开始，循环到 $a = p-1$。在这个讨论中，p 不太大，我们可以快速查看。

尝试一下，试着编写这个代码，看看能找到什么。如果你编码正确，你会发现对于所有的 $a ∈ Fp^*$ ，你永远不会找到一个a 使得 $a^2 = 18$。

我们看到的是，对于 $F^*p$ 的元素，并不是每个元素都有一个平方根。事实上，我们发现对于 $Fp^*$ 中大约一半的元素，没有平方根。

我们说一个整数 x 是一个二次剩余，如果存在一个 a 使得 $a^2 = x \pmod p$。如果没有这样的解，那么整数是一个二次非残差。

换句话说，当 x 模的平方根可以取整数 p 时，x 就是一个二次剩余。

在以下列表中有两个非二次残数和一个二次剩余。

找到二次剩余，然后计算它的平方根。在两个可能的根中，提交较小的一个作为标志。

如果 $a^2 = x$，那么$(- a)^2 = x$。所以如果 x 是有限域中的二次剩余那么 a 总是有两个解。

p = 29
ints = [14, 6, 11]

exp

def judge_qr(a, p):
    tmp = 1
    for i in range((p - 1) // 2):
        tmp = tmp * a % p
    if tmp == 1:
        return True
    else:
        return False
p = 29
ints = [14, 6, 11]

for i in ints:
    print(judge_qr(i, p))
for i in range(100):
    if i * i % p == 6:
        print(i)

提交较小根 solve~

---

挑战 2.0.2 -> Legendre Symbol

---