LOV3

Misc

Corny Kernel

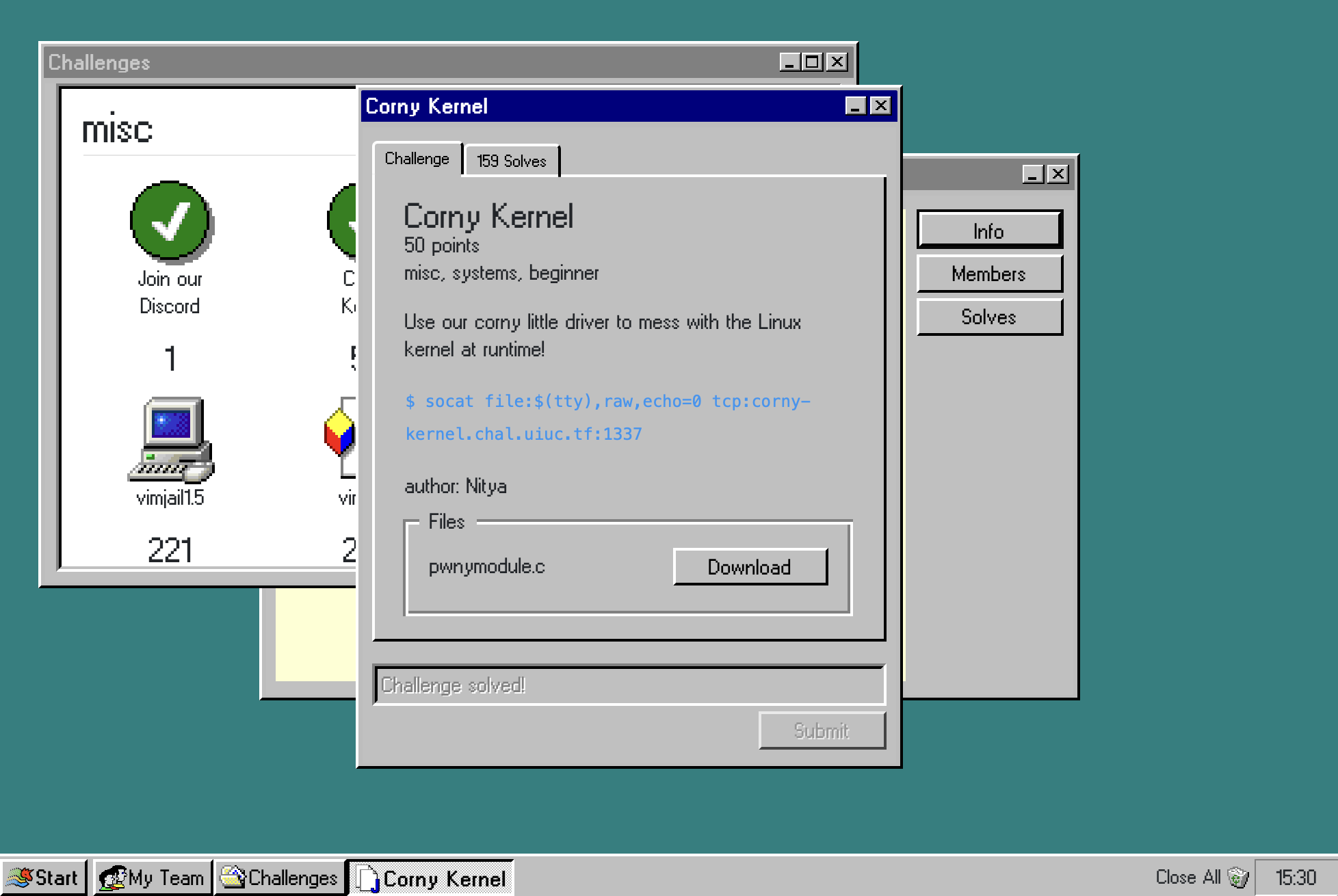
拿到题目看见有源码和一行代码，用来连远端

socat file:$(tty),raw,echo=0 tcp:corny-kernel.chal.uiuc.tf:1337

源码 -> pwnymodule.c

// SPDX-License-Identifier: GPL-2.0-only

#define pr_fmt(fmt) KBUILD_MODNAME ": " fmt

#include <linux/module.h>
#include <linux/init.h>
#include <linux/kernel.h>

extern const char *flag1, *flag2;

static int __init pwny_init(void)
{
	pr_alert("%s\n", flag1);
	return 0;
}

static void __exit pwny_exit(void)
{
	pr_info("%s\n", flag2);
}

module_init(pwny_init);
module_exit(pwny_exit);

MODULE_AUTHOR("Nitya");
MODULE_DESCRIPTION("UIUCTF23");
MODULE_LICENSE("GPL");
MODULE_VERSION("0.1");

根据提示连上远端

执行 ls -la 发现远端已经有了一个名为pwnymodule.ko.gz的内核模块文件，分析 .c 文件后思路为按照以下步骤加载该模块并获取flag的值：

1. 首先，解压缩内核模块文件：

   gunzip pwnymodule.ko.gz
   

   这将解压缩文件并生成一个名为pwnymodule.ko的内核模块文件。

2. 加载内核模块：

   insmod pwnymodule.ko
   

   这将加载内核模块并执行初始化函数。可以看到 flag1

3. 也可以检查系统日志，以查看flag1的值：

   dmesg | tail
   

   flag1的值应该会显示在最后几行的日志中。

4. 查看flag2的值，使用以下命令卸载内核模块，并再次加载它：

   rmmod pwnymodule
   
   insmod pwnymodule.ko
   

5. 检查系统日志，以查看flag2的值：

   dmesg | tail
   

   flag2的值应该会显示在最后几行的日志中。

复制出来拼接就好了 -> uiuctf{m4ster_k3rNE1_haCk3r}

solve~

Crypto

Three-Time Pad

50 points
beginner, crypto

"We've been monitoring our adversaries' communication channels, but they encrypt their data with XOR one-time pads! However, we hear rumors that they're reusing the pads...\n\nEnclosed are three encrypted messages. Our mole overheard the plaintext of message 2. Given this information, can you break the enemy's encryption and get the plaintext of the other messages?"

Author: Pomona

Files:
        c1
        c2
        c3
        p2

对c2和p2 进行xor后得到key, 然后用刚得到的 key 对 c3 进行 xor, 得到明文

exp

# 打开p2 和 c2 xor 找到key
with open('p2', 'rb') as f:
    p2 = f.read()
with open('c2', 'rb') as f:
    c2 = f.read()
from pwn import xor
key = xor(p2, c2)
print(key)
with open('c1', 'rb') as f:
    c1 = f.read()

with open('c3', 'rb') as f:
    c3 = f.read()

m = xor(key, c1)
print(m) # flag不在这里
m = xor(key, c3)
print(m) # 找到flag

solve~

At Home

50 points
crypto, beginner

Mom said we had food at home

Author: Anakin

Files:
        chal.py
        chal.txt

直接在题目上改的exp 如下 (算是一道解方程)

exp

from Crypto.Util.number import getRandomNBitInteger, long_to_bytes

flag = int.from_bytes(b"uiuctf{******************}", "big")

def DEBUG():
    # DEBUG
    print(f"\n{M = }\n{e = }\n{d = }\n")

a = getRandomNBitInteger(256) # 256 bit integer
b = getRandomNBitInteger(256) # 256 bit integer
a_ = getRandomNBitInteger(256) # 256 bit integer
b_ = getRandomNBitInteger(256) # 256 bit integer

M = a * b - 1 # 512 bit integer
e = a_ * M + a # 512 bit integer
d = b_ * M + b # 512 bit integer

DEBUG()

n = (e * d - 1) // M # 512 bit integer

c = (flag * e) % n # 512 bit integer
# 根据这个公式，我们可以得到以下等式：
# flag * e ≡ c (mod n)
# 要求解 flag 的值，我们需要找到 flag 在模 n 意义下的乘法逆元。也就是说，我们需要找到一个整数 x，使得 (x * e) % n = c。
# 可以使用扩展欧几里得算法来计算乘法逆元



print(f"{e = }")
print(f"{n = }")
print(f"{c = }")

e = 359050389152821553416139581503505347057925208560451864426634100333116560422313639260283981496824920089789497818520105189684311823250795520058111763310428202654439351922361722731557743640799254622423104811120692862884666323623693713
n = 26866112476805004406608209986673337296216833710860089901238432952384811714684404001885354052039112340209557226256650661186843726925958125334974412111471244462419577294051744141817411512295364953687829707132828973068538495834511391553765427956458757286710053986810998890293154443240352924460801124219510584689
c = 67743374462448582107440168513687520434594529331821740737396116407928111043815084665002104196754020530469360539253323738935708414363005373458782041955450278954348306401542374309788938720659206881893349940765268153223129964864641817170395527170138553388816095842842667443210645457879043383345869


# 计算M的值
M = (e * d - 1) // n
a = (e * d - 1) % n
b = (a - 1) // M

DEBUG()

def extended_gcd(a, b):
    if b == 0:
        return a, 1, 0
    else:
        gcd, x, y = extended_gcd(b, a % b)
        return gcd, y, x - (a // b) * y

def modular_inverse(a, m):
    gcd, x, _ = extended_gcd(a, m)
    if gcd == 1:
        return x % m
    
flag = (c * modular_inverse(e, n)) % n

print(flag, long_to_bytes(flag))

# print(f"{M = }")

solve~